알자시리즈 - #1 Big-O 표기법(notaion)
알고리즘
자료구조
JavaScript
📝 2019년 05월 01일

Udemy 강의를 듣고 직접 정리한 요약본입니다.
같은 함수의 여러가지 구현을 생각해볼 때, 어떤것이 최고라고 할 수 있을까?
Who Cares?
- 우리의 코드가 성능이 어느정도 되는지 표현 할 수 있는 정확한 단어가 있는것은 중요하다.
- 서로 다른 접근법의 모순을 이야기하는데 유용함
- 우리의 코드가 느려지거나 크래쉬났을때, 코드의 비효율적인 부분을 찾아내는것은 우리 앱의 고통을 덜어줄 수 있다.
- 별로 안중요함 : 인터뷰에 나온다!
예제 : 1부터 n까지 더하는 함수를 가정해보자
// for loop 이용
function addUpTo(n) {
let total = 0;
for (let i = 1; i <= n; i++) {
total += i;
}
return total;
}
//흐른 시간
//1: 1.365799999970477 초
//2: 1.1890000000130385 초//수학 공식 이용
function addUpTo(n) {
return (n * (n + 1)) / 2;
}
//흐른 시간
// 1 : 0.00010000000474974513 초
// 2 : 0.00010000000474974513 초var t1 = performance.now()
addUpTo(1000000000); //
var t2 = performance.now();
console.log(`흐른 시간: ${(t2 - t1)/1000} 초`)'좋다'의 의미는?
-
빠른가 ?
-
적은 메모리 집약? (less memory-intensive)
-
더 나은 가독성 ?
모두다 맞는 말이지만, 1,2 번이 주로 언급하는 문제이고, 1번이 주라고 생각한다.
시간을 측정하면서의 문제점
- 서로다른 머신은 서로다른 시간을 기록한다
- 같은 머신 또한 서로다른 시간을 기록한다!
- 매우 빠른 알고리즘에서 속도측정은 충분히 정확하지 않을 수 있다?
시간을 사용하지 않는다면 뭐로 측정하나?
매우 변수적인초(second)를 카운팅하는것 보다 ⇒ 컴퓨터가 수행하는 간단한 연산자의 갯수를 카운팅하자!

- n의 크기에 관계없이 '3'의 간단한 연산

- 우리가 무엇을 세는지에 따라서 연산자의 갯수는 2n보다 작거나, 5n+2보다 클 수 있다.
- 그러나 정확한 갯수에 상관없이, 연산자의 갯수가 증가함에 따라 n에 비례해서 급격하게 증가한다.
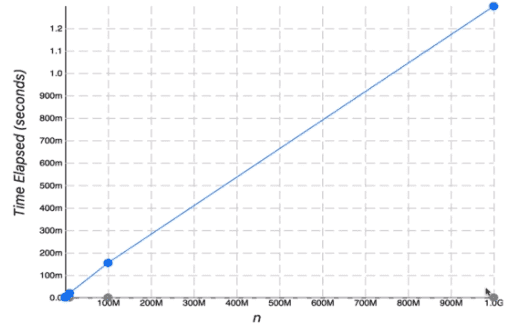
Big O 를 소개하자면..
Big O Notation은 불분명한 카운팅을 형식화하는 방법이다.
인풋이 많아질 수록 알고리즘의 런타임이 어떻게 커지는지에 대해서 형식적으로 말할 수 있게 한다.
우리는 디테일에 대해서 신경쓰지 않을것이다. 오직 트렌드를 신경쓰자
Big O 정의
만약 컴퓨터가 할 간단한 연산의 갯수가 n이 증가하면서 결국 상수 시간 f(n)보다 적다면 알고리즘이 O(f(n))이라고 한다.



Big O 표현법 간단히 하기
- 상수는 신경쓰지 않는다
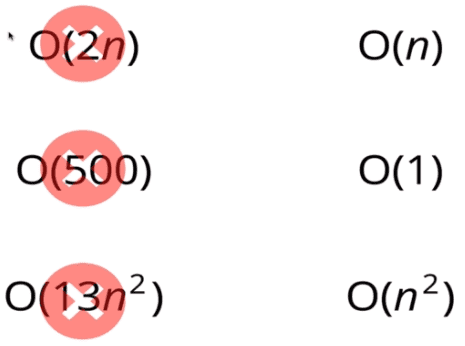
- 작은 숫자는 신경쓰지 않는다
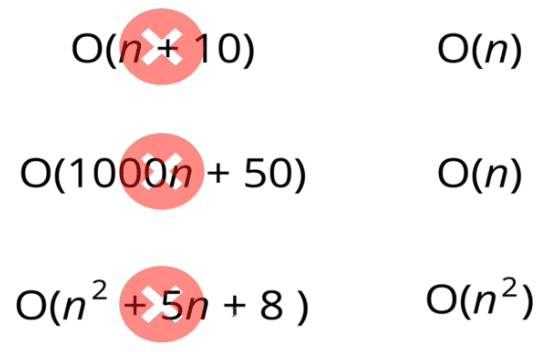
- 산술(arithmetic)연산 ⇒ constant
- 변수 할당 ⇒ constant
- array의 element 접근 (by index) 또는 object의 element 접근(by key) ⇒ constant
- loop에서, 복잡도는 loop 안에서 무슨일이 일어나든간에 loop한 횟수(길이)이다.

⇒ n이 급격하게 커지면 n만큼 커짐

⇒ n이 급격하게 커져도 최대 5번밖에 loop를 돌지 않는다.
Space Complexity(공간복잡도)
우리는 인풋이 늘어남에 따라 어떻게 알고리즘의 런타임을 측정하는지에 대한 ⇒ time complexity(시간 복잡도)에 대해서 이야기했다.
우리는 또한 Big-O notation으로 코드를 실행하기위해 얼마나 많은 추가적인 메모리를 할당해야 하는지에 대한 ⇒ space complexity를 측정할 수 있다.
inputs은 어쩌고 ?
때때로 당신은 인풋에 의해 포함되는 공간을 제외하고, 알고리즘에 의해 요구되는 공간을 언급하는 auxiliary space(구조가 주어진 자료를 저장하기 위해 사용하는 공간) complexity라는 용어를 들어본적이 있을것이다.
우리가 space complexity라고 이야기하는것은 기술적으로 우리는 auxiliary space complexity를 언급하는 것이다. ⇒ 즉 input은 신경쓰지 않는다
알고리즘 내부의 영향을 신경쓰자.
자바스크립트에서 공간복잡도
- 대부분의 primitives(
boolean,numbers,undefiend,null) ⇒ constant space - String ⇒ O(n) space (n은 string 길이)
- 레퍼런스 타입(arrays,object) ⇒ O(n) (n은 배열에서는 배열의 길이, 객체는 key의 갯수)
시간이아니라 공간을 생각하자!
예제


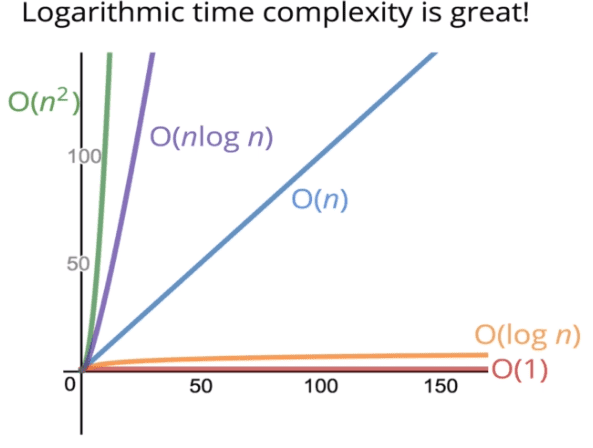
Logarithms
- 우리는 O(1),O(n),O(n^2)과 같은 복잡도를 자주 보겠지만, 가끔은 Big O 표현법이 좀더 복잡한 수학적 표현식을 가질때가 있다. 주로 보이는것이 바로 logarithm이다.
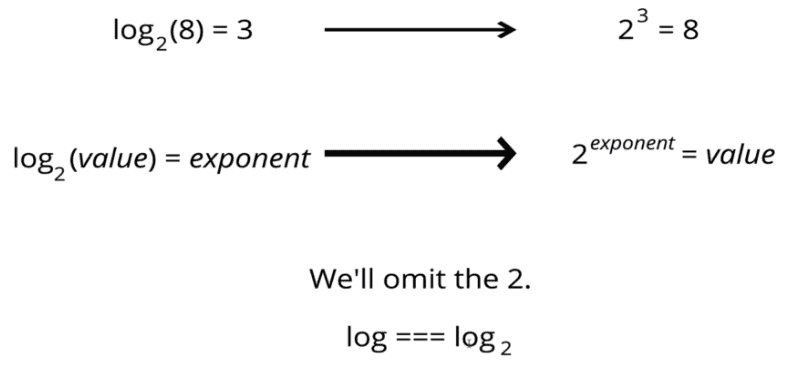
복습
- 알고리즘의 성능을 측정하기 위해서 Big O 표기법을 사용했다.
- Big O 표기법은 알고리즘의 시간/공간 복잡도를 매우 잘 이해시킨다.
- Big O 표기법은 정확도를 신경쓰는게 아니라 일반적인 트렌드를 말한다.(선형? 상수? 이차?)
- (Big O로 측정한) 시간 또는 공간 복잡도는 알고리즘을 실행하는데 사용된 하드웨어가 아니라 오직 알고리즘에 의존한다.
- Big O 표기법은 어디든지 있다. 많은 연습이 필요하다!
